A問題 Edge Checker
方針
a,bの入力値が与えられます。a,bはともに1~10の範囲の整数です。
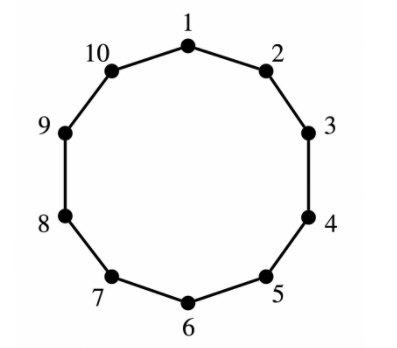
a,bが直接線で結ばれている=隣り合っているかを確認する問題です。
画像を見ると、線で結ばれているということはa,bの差は1になっていることが見て取れます。
(1,10)の組み合わせの時だけは差が9になります。
解答
|
1 2 3 4 5 6 7 8 |
a,b = map(int, input().split()) if abs(a-b)==9: #a,bが1,10の組み合わせの時も線で結ばれているので、Yesを出力 print('Yes') elif abs(a-b)==1: #abs(a-b)とすることでa,bの差の絶対値を調べています。1の場合はYesを出力 print('Yes') else: #a,bが(1,10)と差が1となる組み合わせ以外は線で結ばれていないのでNoを出力 print('No') |
B問題 Count Distinct Integers
方針
何種類の整数があるかを調べる問題です。
入力例1:1 4 1 2 2 1
1,2,4の3種類なので3が答えです。
入力例2:1
1しかないので1が答えです。
入力例3:3 1 4 1 5 9 2 6 5 3 5
1,2,3,4,5,6,9の7種類なので7が答えです。
結局、入力された整数列の内、重複する数値を排除した後の数を数えることになります。
重複の排除にはsetを用います。
解答
|
1 2 3 4 5 |
n = int(input()) A = list(map(int,input().split())) A=set(A) #set(A)とすることで、重複を排除することができる print(len(A)) #重複を排除した後の整数列Aの要素の長さが整数の種類になる |
C問題 Jumping Takahashi
方針
動的計画法を用います。
dpテーブル:dp[i][j]について考えます。
iはジャンプした回数、jはi回目のジャンプ後の座標を示します。
この問題で知りたいことは、N回ジャンプ後に座標Xにいることができるかなので、dp[N][X]==Trueとなるかを調べ、TrueであればYes、FalseでなければNoを出力して解答します。
※True/Falseは1,0など他の文字列・数字でも問題ありません。
続いてN回ジャンプ後に座標Xにいるかをどうやって調べるかについてです。
N回ジャンプ後の座標は、N-1回ジャンプ後の座標と、N回目のジャンプで飛べる距離a,bのみによって決まります。
同じ要領で、N-1回ジャンプ後の座標はN-2回目のジャンプ後の座標と、N-1回目のジャンプで飛べる距離a,bのみによって決まります。
これを繰り返して遡っていけば、各ジャンプ後の座標がどこにあるかをdpテーブルに保存しておくことができます。
保存した各ジャンプ後の座標jがX以下ならTrueとし、Xを超えたらFalseとします。
ジャンプをまだ行っていないとき、つまりdp[0][0]ではTrueとなります。
※dp[0][0]=True ジャンプを行っていないときは座標0にいるため
また、ジャンプをまだ行っていないときは、dp[0][0]以外はFalseになります。
i回目までジャンプを終えた後、次のジャンプでのdp遷移は2通りあります。
①現在地からaだけジャンプ→dp[i+1][j+a]
②現在地からbだけジャンプ→dp[i+1][j+b]
①:j+a<=XならTrue、②:j+b<=XならTrue です。
ジャンプする回数分この2つの状態を繰り返して調べ、n回ジャンプした後に座標XにいられればTrueとします。
i回目のジャンプで座標Xを超えたときは無視します。ジャンプで戻ることはできないからです。※座標をXを通りすぎるとその後何回ジャンプしても座標Xにいることはできません。
解答
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
n,x = map(int, input().split()) dp = [[False]*(x+1) for _ in range(n+1)] dp[0][0] = True for i in range(n): a,b = map(int, input().split()) for j in range(x+1): if dp[i][j]: if j+a<=x: dp[i+1][j+a]=True if j+b <=x: dp[i+1][j+b]=True if dp[n][x] == True: print('Yes') else: print('No') |


コメント