統計検定2級を受験するにあたり、解答時に覚える必要のある公式などを今回の記事でまとめておきます。
テキストやWebサイトでは、試験で必要となる公式がバラバラの場所に記載されているので、このページに一覧としてまとめておき、後から効率よく見直すことを目標とします。
意味を理解するためにはこちらのサイトで勉強するのが非常にオススメです。
歪度
分布が正規分布からどれだけ歪んでいるかを表す。
ヒストグラムで見たときに、山が左側にある場合は正の値、山が道側にある場合は負の値をとる。
・数式
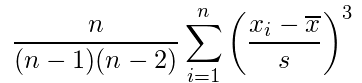
尖度
分布が正規分布からどれだけ尖っているかを表す。
・数式
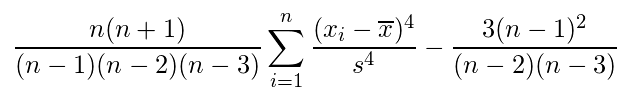
分散
・数式
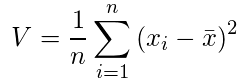
・偏差:各データの平均値との差の合計
・平均偏差:各データの平均値との差の絶対値の平均
・分散:各データの平均値との差の2乗の合計の平均
標準偏差
・標準偏差:分散の正の平方根
・数式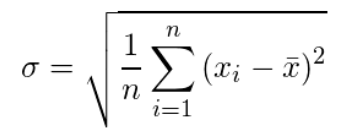
変動係数
単位の異なるデータのばらつきや、平均値に対するデータとばらつきの関係を相対的に評価する際に用いる単位を持たない(=無次元の)数値。
平均値が大きく異なるデータ同士の散らばり方の比較は標準偏差ではできないため、変動係数を用いて比較する。
・数式
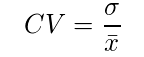
条件付き確率
・P(B)の事象が起こる中でのP(A)が起こる確率
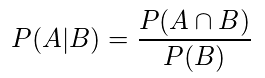
乗法定理
![]()
ベイズの定理
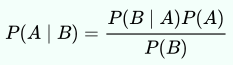
連続型確率分布
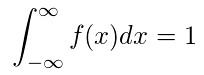
累積分布関数
・離散
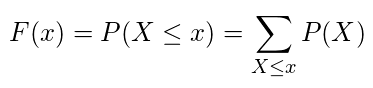
・連続
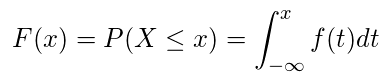
期待値
・離散
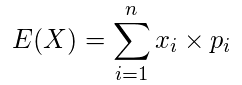
・連続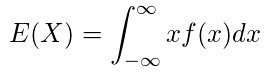
確率変数の分散
X:確率変数
μ:Xの期待値
・離散
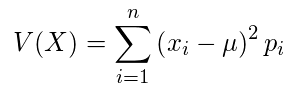
・連続
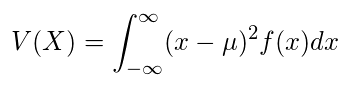
・分散と期待値の関係
確率変数Xの分散は期待値から求めることができる。
E(X^2)は確率変数Xの各値を2乗した場合の期待値
{E(X)}^2はE(X)の2乗
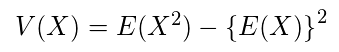
二項分布
ベルヌーイ試行をn回数行い、成功する回数Xが従う分布
・数式
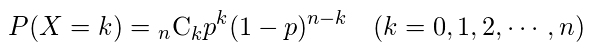
・期待値:E(X) = np
・分散:V(X) = np(1-p)
ポアソン分布
・数式
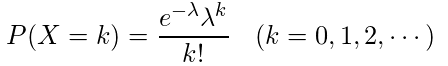
・λ=np
・期待値:E(X) = λ
・分散:V(X) = λ
幾何分布
k回めで初めて成功する確率
・数式
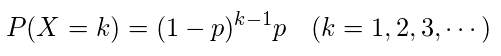
・期待値
E(X)=1/p
・分散
V(X)=(1-p)/p^2
正規分布
・数式
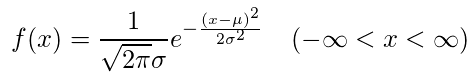
・期待値
E(X)=μ
・分散
V(X)=σ^2
標準正規分布
平均μ=0、分散σ^2=1の時の正規分布
・数式
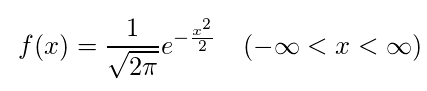
標準化
標準化することで単位や平均値が異なるデータを比較することができる。
X:確率変数
μ:平均
σ:標準偏差では
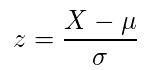
指数分布
ある事象が起こってから次に起こるまでの期間
・数式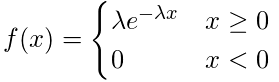
・期待値
E(X)=1/λ
・分散
E(X)=1/(λ^2)
・累積分布関数
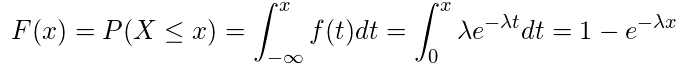
離散一様分布
・離散
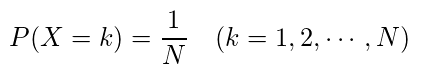
・期待値
E(X)=(N+1)/2
・分散
V(X)=(N^2-1)/12
連続一様分布
・数式
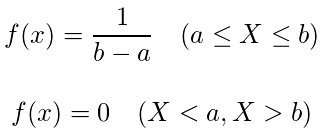
・期待値
E(X)=(a+b)/2
・分散
V(X)=(b-a)/12
・累積分布関数
F(x)=(x-a)/(b-a)
離散型同時確率分布
・数式
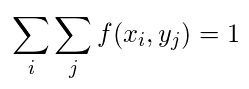
連続型同時確率分布
・数式
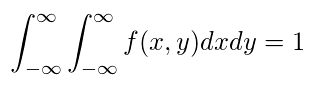
・確率変数が2つある場合の分散
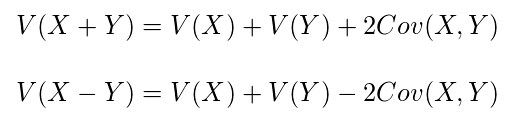
共分散
V(X+Y)=V(X)+ V(Y)+2Cov(X,Y)
Cov(X,Y)=E(XY)-μxμy
相関係数
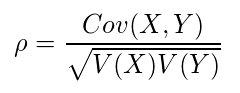


コメント