相関係数
・xとyの相関係数
・分子はxとyの共分散
・分母はxとyの標準偏差の積
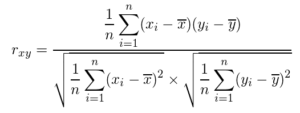
無相関の検定
・帰無仮説は母相関は0であるとする。
・自由度n-2のt分布に従う。
・rは前項の相関係数から求める。
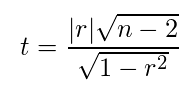
母相関係数の信頼区間
偏相関係数
偏相関係数:疑似相関がある場合に第三の因子の影響を除いた相関係数
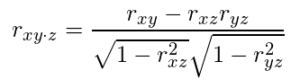
単回帰分析
回帰:目的変数yについて説明変数xを用いた式で表すこと
単回帰式:y=β0 + β1 * x + u
u(誤差):真の回帰式の値と実際のデータとの差
・βの求め方
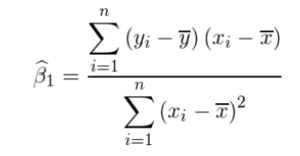
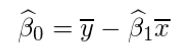
重回帰分析
・回帰式
![]()
偏回帰係数の優位性の検定
・自由度 n-k-1のt分布に従う。
・nはサンプルサイズ、kは説明変数の数
・統計量
分母は標準誤差
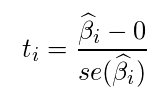
偏回帰係数の信頼区間
・信頼区間の求め方
![]()
予測値と残差
・残差:推定値と実際のデータとの差
・残差の総和は0
・説明変数と残差の積和は0
決定係数
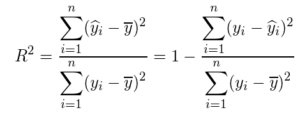
自由度調整済み決定係数
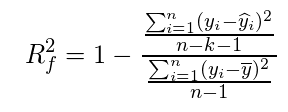
F分布
・F値の求め方
(1)不偏分散の比を計算する。
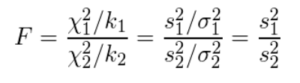
(2)不偏分散がなく、分散のみ与えられている場合は、2標本のそれぞれの不偏分散νを求める。
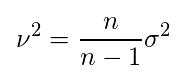
・自由度(n1-1),(n2-1)のF分布に従う。
n1は分子、n2は分母、(値の大きい方を分子にする。)
・期待値
E(X)=n/(n-2) (n>2)
・分散
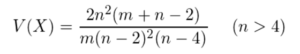
・t分布とF分布の関係
zはN(0,1)の標準正規分布に従う。
Wは自由度nのカイ二乗分布
zとWが独立なとき、自由度nのt分布に従う。
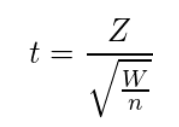
tが自由度nに従うとき、t^2は自由度(1,n)のF分布に従う。

等分散性の検定
・手順
1 仮説を立てる
2つの分散は等しいことを帰無仮説とする。
2 有意水準を決める
3 検定統計量を求める
・値が大きい方を分子にする

4 棄却ルールを決める
5 分布表から読み取る
・両側検定を行う
Whelchのt検定
・2標本のt検定の際、2標本の母分散が等しくないときに用いる。
・t値の求め方
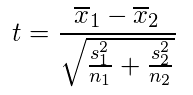
多重共線性
回帰式において、説明変数同士の相関が高い場合、以下の影響などで推定精度が悪くなる。
・分析結果での係数の標準誤差が大きくなる。
・t値が大きくなる
・決定係数が大きくなる
分散分析
・各群の母平均は等しいことを帰無仮説とする
・F分布を用いる
・データ全体の平均が因子の各水準の平均値からどのくらいずれているかを見る。
一元分散分析
・手順
[1]平方和を求める
(1)全体平均と各データの差の二乗和を求める
(2)全体の平均値と因子の各水準の平均値との差の二乗和を求める
(3)因子の各水準の平均値と各データの差の二乗和を求める
(1) = (2)+(3)
[2]自由度を求める
(4)全体の自由度を求める
全体の自由度 = 全てのデータの個数 – 1
(5)要因の自由度を求める
要因の自由度 = 因子の水準 – 1
(6)残差の自由度を求める
残差の自由度 = 全体の自由度 – 要因の自由度
[3]検定
(7)平均平方を求める
平均平方 = 平方和 / 自由度
(8)F値を求める
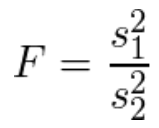
一元配置分散分析では、要因の平均平方を分子とする。
(9)F値から検定を行う。
自由度(要因の自由度,残差の自由度)のF分布で検定する。
片側検定を行う。


コメント